NCERT exemplar class 12 Physics solutions Chapter 1 Electric Charges and Fields

CBSE exemplar class 12 Physics solutions Chapter 1 Electric Charges and Fields

CBSE Exemplar Class 12 Physics Chapter Wise Links

◆ CBSE exemplar class 12 Physics solutions Chapter 1 Electric Charges and Fields

◆ CBSE class 12 Physics exemplar solutions Chapter 2 Electrostatic Potential and Capacitance

◆ CBSE exemplar class 12 Physics solutions Chapter 3 Current Electricity

◆ CBSE Exemplar Class 12 Physics Solutions Chapter 4 Moving Charges and Magnetism

◆ CBSE 12th Physics exemplar solutions Chapter 5 Magnetism and Matter

◆ CBSE exemplar class 12 Physics solutions Chapter 6 Electromagnetic Induction

◆ CBSE exemplar solutions for class 12 Physics Chapter 7 Alternating Current

◆ CBSE exemplar class 12 Physics solutions Chapter 8 Electromagnetic Waves

◆ Class 12 Physics CBSE exemplar solutions Chapter 9 Ray Optics and Optical Instruments

NCERT exemplar class 12 Physics solutions Chapter 10 Wave Optics
NCERT class 12 Physics exemplar solutions Chapter 11 Dual Nature of Radiation and Matter
NCERT exemplar class 12 Physics solutions Chapter 12 Atoms
NCERT 12th Physics exemplar solutions Chapter 13 Nuclei
NCERT exemplar class 12 Physics solutions Chapter 14 Semiconductor Electronics
NCERT exemplar solutions for class 12 Physics Chapter 15 Communication Systems

CBSE Exemplar Class 12 Physics Solutions Chapters-wise Weightage

As far as the CBSE board exam, NEET , JEE Main and other competitive exams are concerned, all the chapters of class 12 Physics CBSE & NCERT exemplar solutions are important. So, a student preparing for class 12 physics will be definitely benefited with CBSE exemplar class 12 Physics solutions.

Table of contents

NCERT Exemplar Class 12 Physics Solutions Chapter 1 MCQI
NCERT Exemplar Class 12 Physics Solutions Chapter 1 very short answer
NCERT Exemplar Class 12 Physics Solutions Chapter 1 short answer
NCERT Exemplar Class 12 Physics Solutions Chapter 1 long answer
Main subtopics of NCERT exemplar class 12 physics solutions chapter 1 Electric Charges and Fields
Important topics, sub-topics, and terms of NCERT Exemplar Class 12 Physics Solutions Chapter 1 Electric Charges and Fields
NCERT Exemplar Class 12 Physics Chapter Wise Links
Important topics to cover for exams from NCERT Exemplar Class 12 Physics Solutions Chapter 1 Electric Charges and Fields

CBSE Exemplar Class 12 Physics Solutions Chapter 1 MCQI

Question:1

In Fig.1.1, two positive charges q 2 and q 3 fixed along the y axis, exert a net electric force in the + x direction on a charge q 1 fixed along the x axis. If a positive charge Q is added at (x, 0), the force on q 1

A. shall increase along the positive x-axis.
B. shall decrease along the positive x-axis.
C. shall point along the negative x-axis.
D. shall increase but the direction changes because of the intersection of Q with q 2 and q 3 .

Answer:

The answer is the option (a)
Explanation: The total force acting on a given charge is the vector sum of individual forces exerted on it by other charges.

Here, the net electrostatic force is in positive x-direction by q 2 and q 3 on qx. The nature of force between q 1 q 2 and q 1 q 3 is attractive. Hence qx is negative.
If possible charge Q is placed at (x,0) the nature of force is attractive between q 1 and Q while in the positive x-direction. Therefore, net force on qx due to q 2 , q 3 and Q is also in the same direction. Hence, the force in qx should increase with the addition of Q at (x,0).

Question:2

A point positive charge is brought near an isolated conducting sphere (Fig. 1.2). The electric field is best given by

A. Fig (i)
B. Fig (ii)
C. Fig (iii)
D. Fig (iv)

Answer:

The answer is the option (a)
Explanation: The electric field lines are always perpendicular to the conducting surface. There are no lines inside the conducting surface, and the electric field lines are always coming out of positive charge and goes into a negative charge. Therefore (a) is the correct answer.

Question:3

The electric flux through the surface

A. in fig. 1.3 (iv) is the largest
B. in fig. 1.3 (iii) the least
C. in fig 1.3 (ii) is same as (iii) but samaller han (iv)
D. is same for all figure

Answer:

Answer: The answer is the option (d)
Explanation: According to Gauss' theorem, the total electric flux out of an enclosed area is equal to charge enclosed divided by permittivity.
Here all the areas are equal; therefore, the equal flux will pass through all of them. Hence, (d) is correct.

Question:4

Five charges q 1 , q 2 , q 3 , q 4 , and q 5 are fixed at their positions, as shown in Fig. 1.4. S is a Gaussian surface. Gauss's law is given by
$\oint_{s} E.ds=\frac{q}{\varepsilon _0}$
Which of the following statements is correct?

A. E on the LHS of the above equation will have a contribution from q 1 , q 5 and q 3 while q on the RHS will have a contribution from q 2 and q 4 only.
B. E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q 2 and q 4 only.
C. E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q 3 and q 5 only.
D. Both E on the LHS and q on the RHS will have contributions from q 2 and q 4 only..
Which of the following statements is correct?

Answer:

The answer is the option (b)
Explanation: The E on LHS of the vector sum of all the five charges while the q on RHS is the normal sum of charges enclosed by the surface, therefore, (b) is correct.

Question:5

Figure 1.5 shows electric field lines in which an electric dipole p is placed as shown. Which of the following statements is correct ?

A. The dipole will not experience any force.
B.The dipole will experience a force towards right.
C.The dipole will experience a force towards left.
D.The dipole will experience a force upwards.

Answer:

The answer is the option (c)
Explanation: Here, the electric field lines are non-uniform, and their strength decreases from left to right. Therefore, the force on -q is more than +q. So, the dipole will experience a force towards the left.

Question:6

A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
A. directed perpendicular to the plane and away from the plane.
B. directed perpendicular to the plane but towards the plane.
C. directed radially away from the point charge.
D. directed radially towards the point charge.

Answer:

The answer is the option (a)
Explanation: The electric field lines are always parallel to the conducting plane; therefore, the lines here will be and directing away from the plane. There are no conducting lines inside the conductor. Hence, (a) is correct.

Question:7

A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed.
A. perpendicular to the diameter
B. parallel to diameter
C. at an angle tilted towards the diameter
D. at an angle tilted away towards the diameter

Answer:

Explanation: In a uniformly positively charged hemisphere, the electric field should be perpendicular on a point away from the center towards the diameter.

CBSE Exemplar Class 12 Physics Solutions Chapter 1 MCQ II

Question:8

If $\oint _{s} Eds =0$ over a surface, then

A. The electric field inside the surface and on it is zero.
B. The electric field inside the surface is necessarily uniform.
C. The number of flux lines entering the surface must be equal to the number of flux lines leaving it
D. All charge must necessarily be outside the surface.

Answer:

The correct answers are the options (c,d)
Explanation: $\phi _{s}= 0$ represents that number is electric field lines entering an area is equal to the number of electric field lines leaving. And also, here $q=0$ ; therefore the charge must be outside the enclosed area.

Question:9

The Electric field at a point is
A. always continuous.
B. continuous if there is no charge at that point.
C. discontinuous only if there is negative charge at that point.
D. discontinuous if there is a charge at that point.

Answer:

The correct answers are the options (b,d)
Explanation: Electric field lines cannot be defined at a point where a charge is present. While at any point electric field will be continuous if only one charge is present in the medium.

Question:6

If there were only one type of charge in the universe, then
A. $\oint_{s}E.ds\neq 0$ on any surface
B. $\oint_{s}E.ds= 0$ if the charge is outside the surface.
C. $\oint_{s}E.ds$ could not be defined.

D. $\oint_{s}E.ds= \frac{q}{\varepsilon _0}$ if charge of magnitude q were inside the surface.

Answer:

The correct answers are the options (b,d)
Explanation: $\phi _{s}E . dS= \frac{q}{\varepsilon _0}$ from Gauss' law. Therefore, if $\phi _{s}E . dS= 0$ then $q=0$ , therefore the net enclosed charge should be 0. And if the charge is outside the surface then also $q=0$ . Therefore, (b,d) are correct.

Question:11

Consider a region inside which there are various types of charges, but the total charge is zero. At points outside the region
A. The electric field is necessarily zero.
B. The electric field is due to the dipole moment of the charge distribution only.
C. The dominant electric field is $\alpha \frac{1}{r^3}$ , for large r, where r is the distance from an origin in this region.
D. The work done to move a charged particle along a closed path, away from the region, will be zero.

Answer:

The correct answers are the options (c,d)
Explanation: There are charges present inside the surface, and their sum is zero. In equation
$\phi _{3}=\int E.dS=\frac{q}{\varepsilon _0}$
E is the electric field due to all the charges present in and out of the gaussian surface. Therefore, there must be dipoles present inside the surface.
So, at any point outside the region w.r.t the dipoles inside the region the dominant electric field $\alpha \frac{1}{r^3}$ for large r.
Also, the electric field is conservative, and work done to move a charge on a closed path away from the region will be zero. Here c and d are correct.

Question:13

A positive charge Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring (Fig. 1.7). Then

A. If q > 0 and is displaced away from the centre in the plane of the ring, it will be pushed back towards the centre.
B. If q < 0 and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring.
C. If q < 0, it will perform SHM for small displacement along the axis.
D. q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0.

Answer:

Answer: The correct answers are the options (a, b, d)
Explanation: As the positive charge is uniformly distributed over the ring, the charge at the centre will be zero. So, no force is exerted on charge at the centre. If the charge is pushed away from the centre, it will experience a force pushing back towards the centre, and if the charge is negative, then it will experience a force towards the ring circumference. Also, the negative charge will be in an unstable equilibrium. So, options a, b, and d are correct.

Question:12

Refer to the arrangement of charges in Fig. 1.6 and a Gaussian surface of radius R with Q at the centre. Then

A. total flux through the surface of the sphere is $\frac{-Q}{\varepsilon _0}$

B. field on the surface of the sphere is $\frac{-Q}{4\pi \varepsilon _0R^{2}}$ .
C. flux through the surface of sphere due to 5Q is zero.
D. field on the surface of sphere due to –2Q is same everywhere.

Answer:

The correct answers are the options (a,c)
Explanation: 5Q charge lies outside the Gaussian surface, hence making no contribution to the electric flux. So, a and c are correct options.

CBSE Exemplar Class 12 Physics Solutions Chapter 1 very short answer

Question:14

An arbitrary surface encloses a dipole. What is the electric flux through this surface?

Answer:

According to Gauss' law

$\phi _s=\int E . dS =\frac{q}{\varepsilon _0}$

where q= enclosed charge. So, +q and -q will cancel each other in a dipole and the sum of the charges will be zero.

Question:15

A metallic spherical shell has an inner radius R 1 and outer radius R 2 . A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface?

Answer:

Q is kept at the center of the spherical cavity. –Q charge is induced at the inner surface and +Q on the outer surface.
The surface density is denoted by σ.
a) The surface charge density on the inner surface is σ1= charge/ Area =
$\frac{-Q}{4\pi R_{2}^{1}}$
b) The surface charge density on the other surface is σ2=
$\frac{+Q}{4\pi R_{2}^{2}}$

Question:16

The dimensions of an atom are of the order of an Angstrom. Thus there must be large electric fields between the protons and electrons. Why, then is the electrostatic field inside a conductor zero?

Answer:

Answer: The electric field inside a conductor is zero because the atoms are of order of am angstrom. While an excess charge can cause electric field to generate inside a conductor.

Question:17

If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.

Answer:

If the total charge is zero enclosed by a surface, it does not necessarily mean that the electric field is also zero enclosed by the surface. The electric field can be perpendicular to the surface. While conversely, it does imply that the electric field is zero on the surface.

Question:18

Sketch the electric field lines for a uniformly charged hollow cylinder shown in Fig 1.8.

Answer:

The side view and the top view of the electric field lines for a uniformly charged hollow cylinder are given below: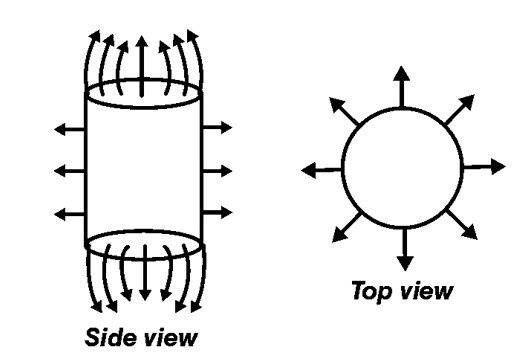

Question:19

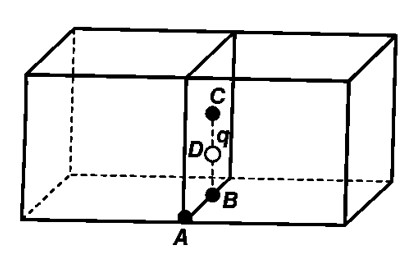
What will be the total flux through the faces of the cube (Fig. 1.9) with side of length a if a charge q is placed at
(a) A: a corner of the cube.
(b) B: mid-point of an edge of the cube.
(c) C: centre of a face of the cube.
(d) D: mid-point of B and C.

Answer:

a) The charge is equally distributed amongst the 8 cubes of a divided cube with sides 2a when the charge is placed at the center of the large cube. Therefore, the total flux through the faces of the cube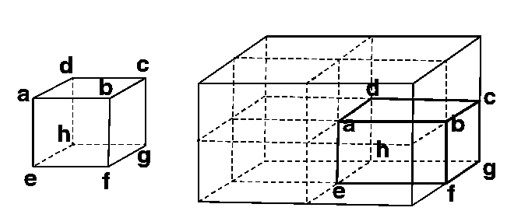 $= \frac{q}{8\varepsilon _0}$

b) If the charge is placed at B, it is equally distributed amongst the 4 cubes. Hence, the total flux through the four faces is $= \frac{q}{4\varepsilon _0}$

c) If the charge is placed at C, then the charge is share by 2 cubes equally, therefore the total flux will be $= \frac{q}{2\varepsilon _0}$

d) If the charge is placed at D, it is distributed amongst two cubes and therefore, the flux through them will be $= \frac{q}{2\varepsilon _0}$

CBSE Exemplar Class 12 Physics Solutions Chapter 1 short answer

Question:20

A paisa coin is made up of Al-Mg alloy and weighs 0.75g. It has a square shape and its diagonal measures 17 mm. It is electrically neutral and contains equal amounts of positive and negative charges. Treating the paisa coins made up of only Al, find the magnitude of equal number of positive and negative charges. What conclusion do you draw from this magnitude?

Answer:

1 molar mass M of Al
$= 6.023 \times 10^{23}\: \: atoms$

A 1 paisa coin containing Al atoms

$= N = \frac{ 6.023 \times 10^{23}}{26.9815 \times 0.75 }= 1.76 \times 10^{22}$
13 electrons and 13 protons are present in Al as it has a charge number of 13.
The magnitude of negative and positive charges $= 3.48 \times 10^{4} C = 34.8 kC$

Question:21

Consider a coin of Example 1.20. It is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges separated by (i) 1 cm , (ii) 100 m ( $\sim$ length of a long building), and (iii) 10 6 m (radius of the earth). Find the force on each such point charge in each of the three cases. What do you conclude from these results?

Answer:

$a)\: \: F1=\frac{\left | q \right |^{2}}{4\pi \varepsilon _0{r_{1}}^{2}}= 1.09\times 10^{23}N$

$CBSE Exemplar Class 12 Physics Solutions Chapter 1 short answer7$

$c)\: \: F3=\frac{\left | q \right |^{2}}{4\pi \varepsilon _0{r_{3}}^{2}}= 1.09\times 10^{7}N$

Question:22

Fig. 1.10 represents a crystal unit of cesium chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners of a cube of side 0.40nm, whereas a Cl atom is situated at the centre of the cube. The Cs atoms are deficient in one electron while the Cl atom carries an excess electron.

(i) What is the net electric field on the Cl atom due to eight Cs atoms?
(ii) Suppose that the Cs atom at the corner A is missing. What is the net force now on the Cl atom due to seven remaining Cs atoms?

Answer:

a) As the chlorine atoms are distributed equally from all the eight corners of the cube from the centre, the net electric field at the centre is therefore zero.
b) The net vector sum of the electric field due the charge A is $E_A + E_{seven \: \: charges} = 0$

Question:23

Two charges q and –3q are placed fixed on x-axis separated by distance 'd'. Where a third charge 2q should be placed such that it will not experience any force?

Answer:

At point P,

$\frac{q}{4\pi \varepsilon _0}x^{2}= \frac{3q}{4\pi \varepsilon _0}\: \: \left ( {x+d} \right )^{2}$

$\left ( {x+d} \right )^{2}=3x^{2}$
On further solving the equation, we will get the distance between the 2q and q charges as
$\frac{d}{2}(1+\sqrt{3})$

Question:24

Fig. 1.11 shows the electric field lines around three-point charges A, B and C.

(a) Which charges are positive?
(b) Which charge has the largest magnitude? Why?
(c) In which region or regions of the picture could the electric field be zero? Justify your answer.
(i) near A, (ii) near B, (iii) near C, (iv) nowhere.

Answer:

i) A and C are positive charges as the electric field lines are protruding out of these two charges.
ii) Charge C has the largest magnitude as it has the greatest number of electric field lines coming out.
iii) The neutral region is in between the charges A and C. Charges C is a stronger charge; therefore the neutral point naturally lies near to A (charge A is a weak charge).

Question:25

Five charges, q each are placed at the corners of a regular pentagon of side 'a' (Fig. 1.12).

(a)
(i) What will be the electric field at O, the center of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?

Answer:

i) The net charge at the centre will be zero as all the charges are equidistant from the centre and they will cancel out each other.
ii) It can be written as that the electric field at O due to A and all other charges is zero. The equation would be as follows:
$\vec{E}_A+\vec{E}_{f\! our\: charges}=0$
Hence $\vec{E}_{f\! our\: charges}=-\vec{E}_A\: \: or \left | \vec{E}_{f\! our\: charges} \right |= \left |\vec{E}_A \right |$
When charge q is removed from A, net electric field at the centre due to
remaining charges $\left | \vec{E}_{f\! our\: charges} \right |= \left |\vec{E}_A \right |=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: \: along\: \: OA$

(iii) If charge q at A is replaced by -q, then electric field due to this negative charge
$\vec{E_{-q}}=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: along \: OA$
Hence net electric field at the centre
$\vec{E_{net}}=\vec{E_{-q}}+\vec{E}_{force \: charge}=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: +\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\:$
$\vec{E}_{net}=\frac{1}{4\pi \varepsilon _0}\frac{2q}{r^{2}}\: \: along \: OA$
b) If pentagon is replaced by a polygon and charge Q at each corner, then also they all will cancel out each other, and the net electric field at O will be zero.

CBSE Exemplar Class 12 Physics Solutions Chapter 1 long answer

Question:26

In 1959, Lyttleton and Bondi suggested that the expansion of the universe could be explained if matter carried a net charge. Suppose that the universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.

(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is proportional to the distance from the centre.

Answer:

a) Let the radius of the Universe be R and assume that the hydrogen atoms are uniformly distributed. The expansion will only occur if the Coulomb repulsion is larger than the gravitational attraction at a distance R
The Hydrogen atom contains one proton and one electron charge on each hydrogen atom
$e_H=e_P+e=-(1+y)e+e=-ye=\left | ye \right |$
Let E be electric field intensity at distance R, on the surface of the sphere, then according to Gauss' theorem,
$\\\oint \vec{E}.d\vec{S}= \frac{q_{enclosed}}{\varepsilon _0}\\ \\ \Rightarrow E(4\pi R^2)=\frac{4}{3}\frac{\pi R^3 N\left | ye \right |}{\varepsilon _0}\\ \\ \Rightarrow E=\frac{1}{3}\frac{ N\left | ye \right |R}{\varepsilon _0}.........1$

Question:31

Total charge –Q is uniformly spread along the length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.

(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.

Answer:

Let the charge q is displaced slightly by $z\left ( z< < R \right )$ along the axis of ring. Let force on the charge q will be towards O. The motion of charge q will be simple harmonic, it the force on charge q must be proportion to z and is directed towards O.
Electric field at axis of the ring at a distance z from the centre of ring
$E=\frac{1}{4\pi \varepsilon _0}\frac{Q_z}{\left ( R^2+Z^2 \right )^{3/2}};$ towords O
the net force on the charge $F_{net}=qE$
$F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{\left ( R^2+Z^2 \right )^{3/2}};$
$\Rightarrow$ $F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}}$
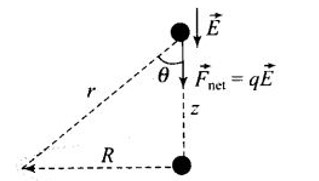
As $z<<R\: then,$
$\Rightarrow$ $F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}}$ or $\vec{F}_{net}=-K\vec{z}$
Where $K=\frac{Qq}{4\pi \varepsilon _{0}R^{3}}=constant$
Clearly, the force on q is proportional to the negative of its displacement. Therefore the motion of q is simple harmonic.
$\\\omega \sqrt{\frac{K}{m}}\: and\: T=\frac{2\pi}{\omega }=2\pi\sqrt{\frac{m}{K}}\\T=2\pi\sqrt{\frac{m4\pi \varepsilon _0\: R^3}{Qq}} \\T=2\pi\sqrt{\frac{4\pi \varepsilon _0\: m\: R^3}{Qq}} \\$

Question:30

Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x (x<<d) perpendicular to the line joining the two fixed charged as shown in Fig. 1.14. Show that q will perform simple harmonic oscillation of time period.

Answer:

Let the charge q is displaced slightly by $x(x<<d)$ perpendicular to the line joining the two fixed charges. The net force on the charge q will be towards O.The motion of charge -q to be simple harmonic if the force on charge q must be proportional to its distance from the centre O and is directed towards O.
The net force on the charge $F_{net}= 2F \cos\theta$
Here $F=\frac{1}{4\pi \varepsilon _0}\frac{q(q)}{r^2}= \frac{1}{4\pi \varepsilon _0}\frac{q^2}{\left ( d^2+x^2 \right )}$
And $\cos \theta =\frac{x}{\sqrt{x^2+d^2}}$
Hence, $F_{net}=2 \left [ \frac{1}{4\pi \varepsilon _0}\frac{q^2}{\left ( d^2+x^2 \right )} \right ]\left [ \frac{x}{\sqrt{x^2+d^2}} \right ]$
$= \frac{1}{2\pi \varepsilon _0}\frac{q^2x}{\left ( d^2+x^2 \right )^{3/2}}=\frac{1}{2\pi \varepsilon _0}\frac{q^2x}{d^3\left ( 1+\frac{x^2}{d^2} \right )^{3/2}}$
As $x<<d, then F_{net}=\frac{1}{2 \pi \varepsilon _0}\frac{q^2x}{d^3}\: or \: F_{net}=Kx$
i.e. force on charge q is proportional to its displacement from the centre O and it is directed towards O.
Hence, the motion of charge q would be simple harmonic, where
$\omega = \sqrt{\frac{K}{m}}\\ and \: T=\frac{2 \pi }{\omega}=2 \pi\sqrt{\frac{m}{K}}$
$\Rightarrow T= 2 \pi \sqrt{\frac{m.4 \pi \varepsilon _0d^3}{2q^2}}=\left [ \frac{8 \pi^3 \varepsilon _0md^3}{q^2} \right ]^{1/2}$

Question:29

There is another useful system of units, besides the SI/mks system, called the cgs (centimetre-gram-second) system. In this system, Columb's law is given by

$F=\frac{Qq}{r^2}$

where the distance r is measured in $cm (= 10^{-2} m)$ , F in dynes $(=10^{-5} N)$ and the charges in electrostatic units (es units), where 1es unit of charge

$\frac{1}{3}\times10^{-9}C$
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by $c = 2.99792458 \times 10^8 \: m/s$ . An approximate value of c then is $c = [3] \times 10^8 m/s.$
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne) 1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge $= x\: C,$ where x is a dimensionless number. Show that this gives

$\frac{1}{4\pi\epsilon_0}=[3]^2\times10^{9}\frac{Nm^2}{C^2}$

Answer:

$(i)$ Acording to relation,
$F =\frac{Qq}{r^2}= 1dyne= \frac{\left [ esu\; of\: chaarge \right ]^2}{\left [ 1cm \right ]^{2}}$
So, 1 esu of charge
$=\left ( 1dyne \right )^{1/2}\times 1 cm$
$F^{1/2}.L=\left [ MLT^{2} \right ]^{1/2}\left [ L \right ]= \left [ M^{1/2}L^{3/2}T^{1} \right ]$
$\Rightarrow$ Hence, [1 esu of charge] = $M^{1/2}L^{3/2}T^{1}$
Thus the charge in C.G.S. unit (in esu) is represented in terms of fractional power 1/2 of M and 3/2 of L.
$(ii)$ If two charge each of magnitude 1 esu separated by 1 cm, Coulomb force on the charge is 1 dyne = $10^{-5}N.$
Let 1 esu of charge =x C, where x is a dimensionless number. We can consider a situation, two charges of magnitude x C separated by $10^{-2}m.$
The force between the charge
$F=\frac{1}{4 \pi \varepsilon _0}\frac{x^{2}}{\left ( 10^{-2} \right )^{2}}= 1dyne=10^{-5}N$
$\therefore \frac{1}{4 \pi \varepsilon _0}= \frac{10^{-9}}{x^{2}}\frac{Nm^{2}}{C^{2}}$
Taking,
$\\x=\frac{1}{\left | 3 \right |\times 10 ^{9}},\\ We \: get\: \: \frac{1}{4\pi \varepsilon _0}=10^{-9}\times \left | 3 \right |^{2}\times 10^{18} \\ \frac{1}{4\pi \varepsilon _0}=9\times 10^{9}\frac{Nm^{2}}{C^{2}}$

Question:28

Two fixed, identical conducting plates $(\alpha and \beta )$ , each of surface area S are charged to –Q and q, respectively, where $Q > q > 0$ . A third identical plate ( $\gamma$ ), free to move is located on the other side of the plate with charge q at a distance d (Fig 1.13). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst $(\beta \: and\: \gamma )$

(a) Find the electric field acting on the plate $\gamma$ before the collision.
(b) Find the charges on β and $\gamma$ after the collision.
(c) Find the velocity of the plate $\gamma$ after the collision and at a distance d from the plate β.

Answer:

(a) Net electric field field at plate $\gamma$ before collision is vector sum of electric field at plate $\gamma$ due to plate $\alpha\: and\: \beta$ .
The electric field at plate $\gamma$ due to plate $\alpha$ is $\vec{E}_1= \frac{Q}{S(2\varepsilon _0)}(-\hat{i}),$

The electric field at plate $\gamma$ due to plate $\beta$ is $\vec{E}_2= \frac{q}{S(2\varepsilon _0)}(\hat{i}),$
Hence the net electric field at plate $\gamma$ before collision is
$\\ \vec{E}=\vec{E}_1+\vec{E}_2= \frac{q-Q}{S(2\varepsilon _0)}(\hat{i}),\\ \\ \vec{E}=\vec{E}_1+\vec{E}_2= \frac{Q-q}{S(2\varepsilon _0)}(\hat{i}),$
Or $\frac{Q-q}{S(2\varepsilon _0)}$ to the left, if $Q>q$

(b) During collision, plates $\alpha\: and\: \beta$ are in contact with each other, hence their potential becomes the same.
Suppose charge on plate $\beta \: is\: q_1\:$ and charge on plate $\gamma \: is\: q_2\:$ . at any point O , in between the two plates, the electric field must be zero.
Electric field at O due to $\alpha$ ,
$\vec{E}_\alpha = \frac{Q}{S(2\varepsilon _0)}\left (- \hat{i} \right )$
Electric field at O due to $\beta$ ,
$\vec{E}_2 = \frac{q_1}{S(2\varepsilon _0)}\left ( \hat{i} \right )$
Electric field at O due to $\gamma$ ,
$\vec{E}_\gamma = \frac{q_2}{S(2\varepsilon _0)}\left (- \hat{i} \right )$
As the electric field at O is zero, therefore
$\frac{Q+q_2}{S(2\varepsilon _0)}=\frac{q_1}{S(2\varepsilon _0)}\\ \\ \because Q+q_2=q_1$
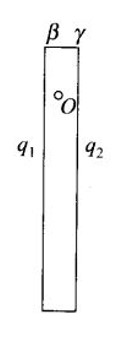
As there is no loss of charge on collision,
$Q+q=q_1+q_2$
On solving Equ. (1) and (2) We get
$q_1=(Q+q/2)=$ Charge on plate $\beta$

$q_1=(q/2)=$

Charge on plate $\gamma$

(c) Let the velocity be $\nu$ at the distance d from plate $\beta$ after the collision.
If m is the mass of the plate $\gamma$ , then the gain in K.E. over the round trip must be equal to the work done by the electric field.
After the collision, electric field at plate $\gamma$ is
$\vec{E}_2= \frac{Q}{2\varepsilon _0S}(-\hat{i}),+\frac{\left ( Q+q/2 \right )}{2\varepsilon _0S}\hat{i}=\frac{\left ( q/2 \right )}{2\varepsilon _0S}\hat{i}$
Just before collision, electric field at plate $\gamma$ is
$\vec{E}_1= \frac{Q-q}{2\varepsilon _0S}\: \hat{i}.$
If F1 is force on plate before collision., then
$F_1=\vec{E}_1Q= \frac{\left ( Q-q \right )Q}{2\varepsilon _0S}\: \hat{i}\: and\: F_2=\vec{E}_2\frac{q}{2}= \frac{\left ( \frac{q}{2} \right )^{2}}{2\varepsilon _0S}\: \hat{i}$
Total work done by the electric field is the round trip movement of plate $\gamma$ ,
$W=(F_1+F_2)d$
$=\frac{\left [ \left ( Q-q \right )Q+\left ( q/2 \right )^{2} \right ]d}{2\varepsilon _0S}=\frac{\left ( Q-q/2 \right )^{2}d}{2\varepsilon _0S}$
If m is the mass of plate $\gamma$ , the KE gained by the plate =
$\frac{1}{2}m\nu ^2$
According to work energy principle,
$\frac{1}{2}m\nu ^2=W \Rightarrow \frac{1}{2}m\nu ^2=\frac{\left ( Q-q/2 \right )^{2}d}{2\varepsilon _0S}$
$\Rightarrow \nu =\left ( Q-q/2 \right )\left ( \frac{d}{m\varepsilon _0S} \right )^{1/2}$

Question:27

Consider a sphere of radius R with charge density distributed as

$\rho (r) = kr for r \leq R\\ = 0\: f\! or \: r >R .$
a) Find the electric field at all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero? Assume that the introduction of the proton does not alter the negative charge distribution.

Answer:

a) The charge density distribution expression in the sphere tells that the electric field is radial.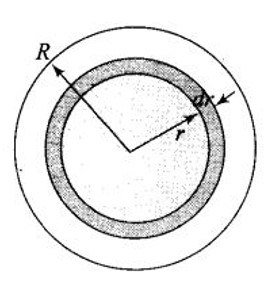

Let us consider a sphere S of radius R and two hypothetic spheres of radius $r< R$ and $r> R$ .
Let us first consider for point $r< R$ , electric field intensity will be given by,
$\oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho \: dV$
Here $dV =4\pi r^2\:dr$
$\Rightarrow \oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}4 \pi K \int_{0}^{r}r^3dr\left ( \because \rho \left ( r \right )=Kr \right )$
$\Rightarrow \left ( E \right )4 \pi r^2= \frac{4 \pi K}{\varepsilon _0}\frac{r^4}{4}$
We get
$E= \frac{1}{4\varepsilon _0}Kr^2$
As charge density is positive, it means the direction of E is radially outwards.

Now consider points $r>R$ , electric field intensity will be given by
$\oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho dV$
$\Rightarrow E(4 \pi r^2)= \frac{4 \pi K}{\varepsilon _0}\int_{0}^{R}r^3dr=\frac{4 \pi K}{\varepsilon _0}\frac{R^4}{4}$
Which gives $E=\frac{K}{4 \varepsilon _0}\frac{R^4}{r^2}$
Here also the charge density is again positive. So, the direction of E is radially outward.
(b) The two proton must be placed symmetrically on the opposite sides of the centre along a diameter. This can be shown by
the figure given below. Charge on the sphere,

$\\q=\int_{0}^{R}\rho dV= \int_{0}^{R}\left ( Kr \right )4 \pi r^2dr\\ \\ q=4 \pi K\frac{R^4}{4}2e\\ \\\because K=\frac{2e}{\pi R^4}$

The proton 1 and 2 are embedded at distance r from the centre of the sphere as shown, then attractive force on proton 1 due to charge
distribution is
$F_1=eE=\frac{-eKr^2}{4\varepsilon _0}$
and repulsive force on proton 1 due to proton 2 is
$F_2=\frac{e^2}{4 \pi\varepsilon _0 (2r)^2}$
Net force on proton 1, $F=F_1+F_2$
$F=\frac{-eKr^2}{4\varepsilon _0}+\frac{e^2}{16 \pi \varepsilon _0r^2}$
Thus, net force on proton 1 will be zero, when
$\frac{er^22e}{4\varepsilon _0 \pi R^4}= \frac{e^2}{16 \pi \varepsilon _0r^2}$
$\Rightarrow r^4= \frac{R^4}{8}$
Hence the protons must be at a distance $r=\frac{R}{(8)^{1/4}}$ from the centre.

The NCERT Exemplar solutions for Class 12 Physics Chapter 1 provided here are very useful and detailed from the point of view of aiding practice, preparation and working for Board exams as well as the JEE exams.

NCERT exemplar class 12 Physics solutions Chapter 1 Electric Charges and Fields

CBSE Exemplar Class 12 Physics Solutions Chapters-wise Weightage

CBSE Exemplar Class 12 Physics Solutions Chapter 1 MCQI

CBSE Exemplar Class 12 Physics Solutions Chapter 1 very short answer

CBSE Exemplar Class 12 Physics Solutions Chapter 1 short answer

CBSE Exemplar Class 12 Physics Solutions Chapter 1 long answer

Post a Comment

CBSE Board Class 12 Business Studies 2024 Question Papers, and Answer Key

Contact Form